7月22日至8月19日,由我校科技处、科协主办,数学学院承办的“西北大学创新论坛”在腾讯会议线上举行,赵云等10位教授为我校相关专业师生代表做了报告。
赵云教授回顾了单个连续函数的遍历优化研究的最新进展(包括从属原理,0温度极限,遍历优化中通有的性质),遍历优化关心任何连续函数的最大遍历平均问题,对满足特殊条件的系统如扩张系统,拓扑双曲系统,Lipschitz系统,Jenkinson,Morris,Contreras展开了大量原创性研究,初步解决了物理学家关于具有混沌性质的系统,最大遍历平均测度的唯一性以及支撑在周期测度的猜测。
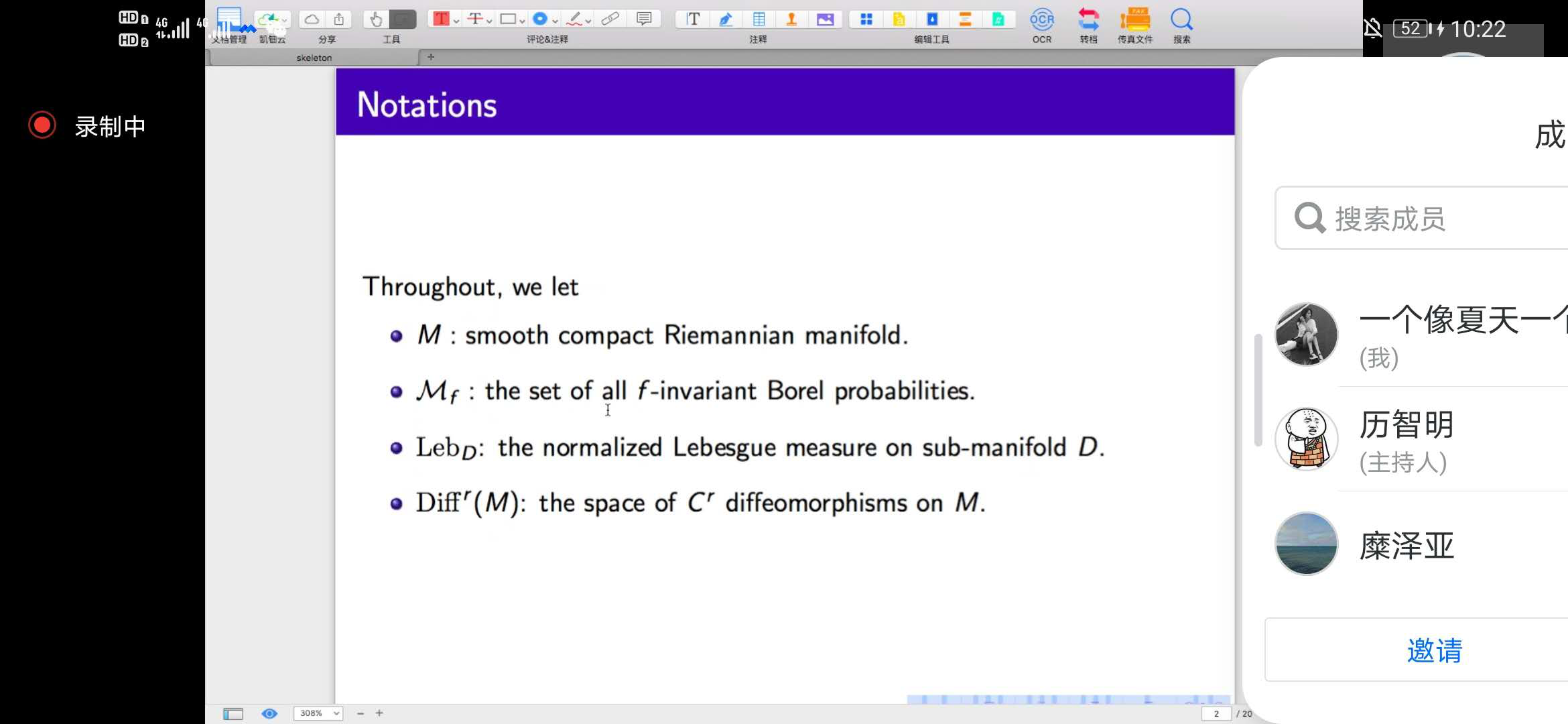
糜泽亚教授从基本定义、符号开始(包括光滑紧的黎曼流形、不变的概率测度、Lebesgue测度、微分同胚等,),娓娓道来。首先,对于底空间是光滑、紧的黎曼流形的动力系统,详细讲述了关于测度的Gibbs-u-平衡态、物理测度、SRB测度的定义、几何意义及研究历史。介绍了部分双曲系统的定义、一致双曲系统的性质和研究现状。其次,介绍了部分双曲系统中的Gibbs-cu-平衡态的定义及相关结论。详细讲解了光滑流形上映射的skeletons的定义,并给出部分双曲系统上存在映射的skeletons的一个重要结论、部分双曲系统上存在映射的skeletons和物理测度的关系,以及不同的动力系统上物理测度的连续性的结论。
吴伟胜教授详细讲解了测地流的相关背景知识,包括Jacobi场,Sasaki度量,Liouville测度相关定义,以及非负曲率流形上侧地流的 Cartan-Hadamard定理,常负曲率流形的例子,无穷远点的Cone拓扑,共轭点,焦点等相关术语。随后又针对侧地流,在对双曲性,稳定流形,不稳定流形,拓扑熵的等价刻画,最大熵测度,遍历性等动力系统的背景知识进行了详细讲解。
杨忠强教授介绍了研究函数空间拓扑结构的动机在于寻找两个拓扑空间之间映射所构成的集合,在赋予自然拓扑后的同胚空间并逐次展开了紧致空到实数空间R的连续映射赋予一致收敛拓扑、逐点收敛拓扑和紧开拓扑时函数空间的同胚问题,并对这些问题的历史和发展过程以及背景知识进行了详细讲解。
朱玉峻教授介绍了动力系统Zk-作用的扩充,包括Zk-作用的几何直观,Rk中子空间的加厚,符号系统、线性诱导作用、光滑作用扩充的例子等相关背景知识,在此基础上朱玉峻教授介绍了自己关于子系统Zk+-作用向前扩充问题的研究,通过“编码”技术得到了最新的成果。
田学廷介绍了与以往对动力系统的研究(回复性,传递性,物理性质,Brikhoff时间平均,李雅普诺夫指数等)的不同之处,该报告关注轨道结构,即长时间的轨道行为(见图2)。研究轨道结构的工具是拓扑熵,混沌,通有性。其次,介绍了动力系统研究中的定义,包括周期点,几乎周期点,点传递,非游荡点,回复点等的定义及它们之间的关系。并给出了新的定义,包括x-ξ-accessible, ξ-ω极限集等,并给出新定义的点集与其它点集之间的关系,得出结论对于X中的任意一点x,x 的轨道满足将近64种轨道行为,其中60种轨道行为在测度意义下是0测集。提出问题,如何区分这些0测集?试图通过拓扑熵和混沌来区分0测集。由此,给出了类似于定义Hausdorff维数形式的拓扑熵的定义(这种熵比用分离集和张成集定义的拓扑熵更适合在分形集上定义),混沌的定义,并得出了对于传递的Anosov系统轨道结构的一些结论。
陈二才教授从三篇参考文献引入主题,首先介绍了概率测度、不变测度、遍历测度、经验测度的定义,Bowen度量、p-Wasserstein度量、Levy-Prokhorov度量,及维数、Packing维数、盒维数、metric order的定义等。并给出他们之间的相关关系,如metric order(度量序)是被底空间的合维数控制的;对于黎曼流形,当系统是扩张的Repeller时,盒维数和Hausdorff维数相等。
廖刚教授介绍了符号表示的历史,及符号系统对研究复杂系统的帮助,用符号提升对复杂系统进行编码的方法,及在编码过程中遇到的问题等。其次详细介绍了C∞无穷光滑系统有本质的符号提升,渐近扩展的系统有本质的符号提升,每一个Cr的系统(r>1)存在符号提升,但当r非无穷大时没有本质符号提升。紧的三维流行M上的Cr(r>1)系统存在符号提升。
李健教授介绍了平均等度连续性的相关背景知识,包括离散谱、平均李雅普诺夫稳定、上密度相关定义及其性质。同时李健教授介绍了自己对平均李雅普诺夫稳定系统是否存在离散谱的公开问题的研究成果,并详细讲解了证明的想法和关键技术,后来该成果得到他人进一步推进,回答了李健教授提出的极小平均等度连续系统是否Weyl平均等度连续的问题。
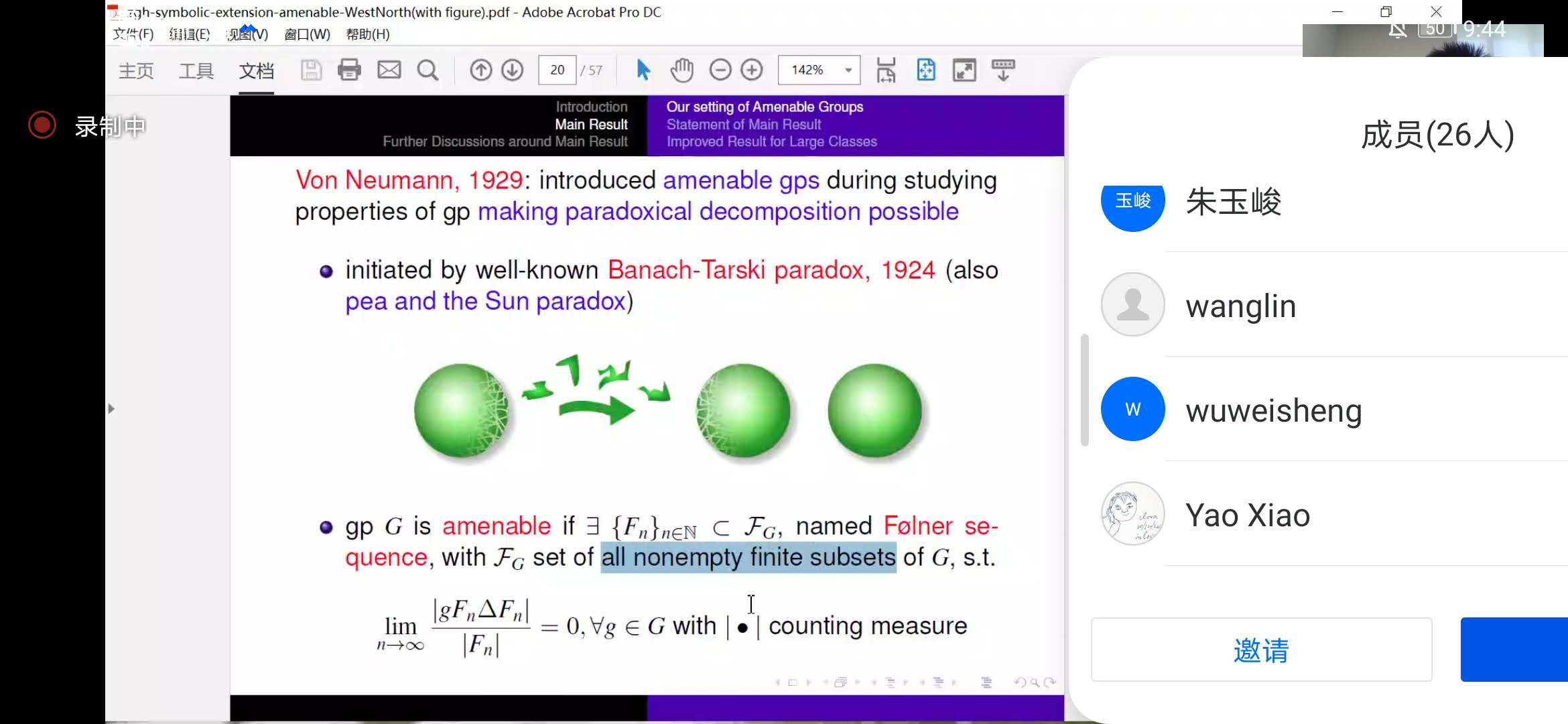
张国华教授运用通俗的语言,介绍了拓扑动力系统、拓扑群作用、符号动力系统的定义。详细介绍了符号动力系统的重要性、符号动力系统的最早提出以及对符号动力系统的研究历史,并通过借助机械表和电子表的对比,来让我们很好地体会研究符号动力系统在研究一般动力系统中作用与差别。介绍了群作用下符号动力系统上的全移位,详细讲解了Amenable群定义、自由群定义、Folner序列的定义,Amenable群理论的发展,特别提出了一个有名的悖论。其次,详细讲解了符号扩张理论(包括扩张的定义,符号扩张的目的是想通过符号动力系统来直观地研究一般动力系统等),衡量符号扩张程度的量,即拓扑熵及引入测度的必要性,并介绍了与测度相关的重要结论。
报告会精彩纷呈,参会师生受益匪浅。